

2026年も半月が経過しました。みなさまいかがお過ごしでしょうか。
今回は、今年の年賀状問題の解答・解説をお知らせします。
問題はこちらでした。

解答
【小学校低学年向け 】72個
【小学校高学年以上向け 】4106702個
解説
線分図を使って考えます。
例に挙がっている29÷7=4あまり1と29÷6=4あまり5をそれぞれ線分図にすると、以下の通りになります。
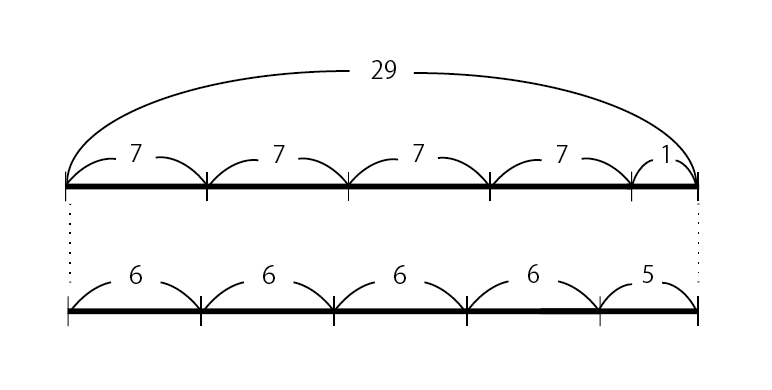
商が4ということは、割る数が4つ入っていることになりますから、割る数を1増やすと余りは4減り、割る数を1減らすと余りは4増えることがわかります。
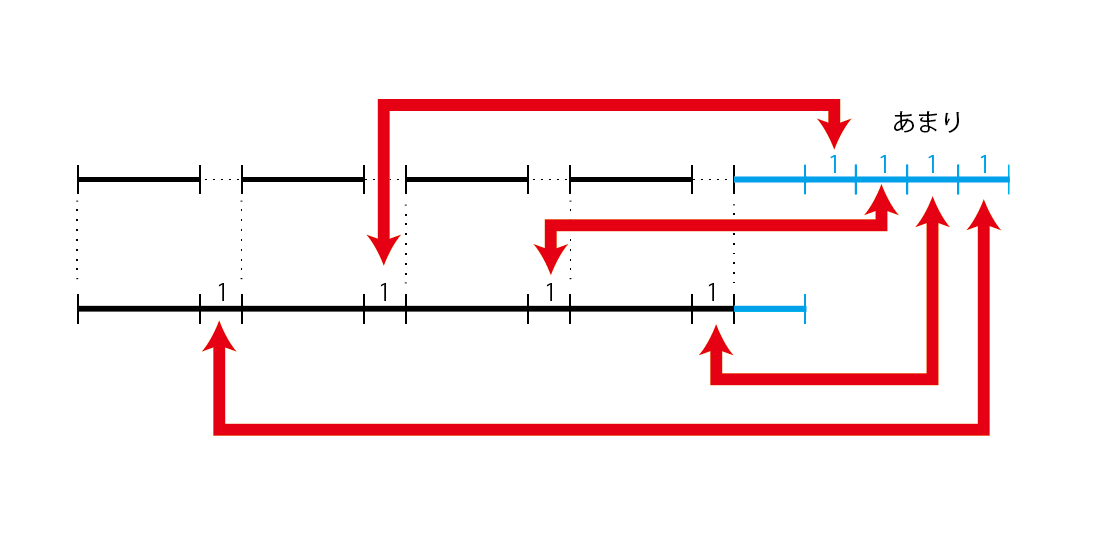
ここで、13÷3=4あまり1のときを考えましょう。
あまりが1なのであまりを4へらすことができません。そのため、割る数を1増やすことはできません。また、割る数を1減らすと割る数は2となり、5あまる、というのは不適となります。
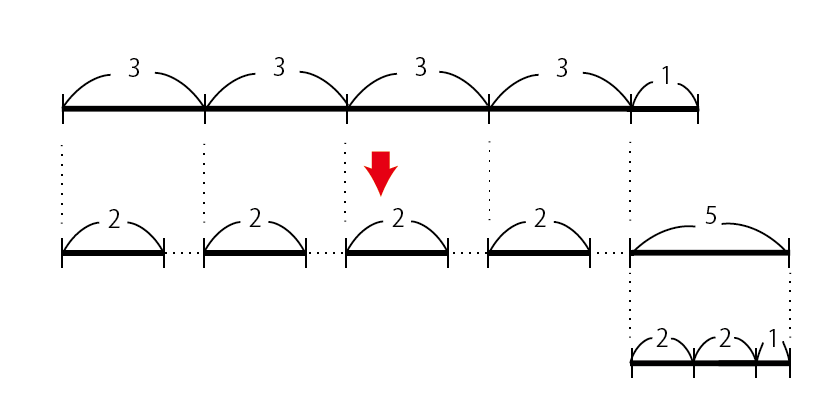
これらより、商が4の場合、余りが0~3で、余り+4が割る数-1以上→余り+5が割る数以上、という条件を満たせばよいことがわかります。
同様に考えると、商が8の場合は、余りが0~7で、余り+9が割る数以上になるのは何通りあるか数えれば良いことになります。
割る数が1→余りは0 1通り
割る数が2→余りは0・1 2通り
割る数が3→余りは0・1・2 3通り
…
割る数が8→余りは0~7の8通り
割る数が9→余りは0~7の8通り
割る数が10→余りは1~7の7通り(余りが0だと割る数が9であまり8が成立)
割る数が11→余りは2~7の6通り
…
割る数が16→余りは7 の1通り
よって(1+2+3+4+5+6+7+8)×2=72通り
商が2026のときも考え方は同じように考えますが、4年生以上は等差数列の和の公式をうまく使うと(2026+1)×2026÷2×2=2027×2026=4106702個となります。
どちらの問題も9×8、2027×2026と簡単な計算式になりました。規則が見つかるときは背景になにか隠れていることが多いです。
実は、上の解説と別の考え方をすると、9×8、2027×2026はすぐに見つかります。
どうやって考えれば良いのか、算数自慢の生徒は上の解説をもとに再度考えてみましょう。