

先日1月16日、年賀状問題の追加問題を掲載しました。
今回はその追加問題の解答・解説です。
「2けた以上の整数で、隣り合う2けたの数字の差がすべて3以下である。」
例えば、2025はヘビ数ですが、2026は十の位と一の位の差が4なのでヘビ数ではありません。
1.ヘビ数を小さい方から順に並べたとき、2025は何番目ですか。
2.ヘビ数を小さい方から順に並べたとき、2025番目の整数はいくつですか。
答え (1)572番目 (2)7798
まずは2けたの場合を書き出して調べてみます。
本来数えなくてもよい十の位が0の場合も書いていますが、後で使うことになります。
0?:00, 01, 02, 03 →4個
1?:10, 11, 12, 13, 14 →5個
2?:20, 21, 22, 23, 24, 25 →6個
3?:30, 31, 32, 33, 34, 35, 36 →7個
4?:41, 42, 43, 44, 45, 46, 47 →7個
5?:52, 53, 54, 55, 56, 57, 58 →7個
6?:63, 64, 65, 66, 67, 68, 69 →7個
7?:74, 75, 76, 77, 78, 79 →6個
8?:85, 86, 87, 88, 89 →5個
9?:96, 97, 98, 99 →4個
十の位が0の場合を除き、2けたのヘビ数は全部で54個あることがわかります。
次に、3けたの場合を調べてみます。
全部書き出すのは大変なので、工夫を考えてみましょう。
例えば、百の位が3のとき、十の位は0, 1, 2, 3, 4, 5, 6のどれかなので、次のような関係が成り立ちます。
(3??の個数)=(30?の個数)+(31?の個数)+(32?の個数)+(33?の個数)+(34?の個数)+(35?の個数)+(36?の個数)
この中の1つである(30?の個数)に注目すると、下2けた「0?」がヘビ数であれば全体の3けたの整数「30?」としてもヘビ数であることから、
(30?の個数)=(0?の個数)
とわかります。他も同様にして、
(3??の個数)=(0?の個数)+(1?の個数)+(2?の個数)+(3?の個数)+(4?の個数)+(5?の個数)+(6?の個数)
=4+5+6+7+7+7+7=43個
百の位で場合分けして同様に考えると、ヘビ数の個数を以下のような表にまとめることができます。
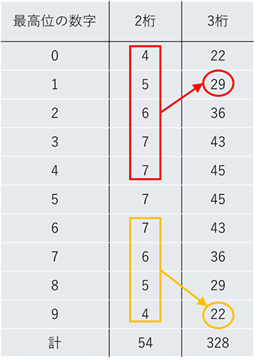
(赤枠は「1??の個数」、黄枠は「9??の個数」の計算例。「計」の欄は最高位の数字が0の場合を除いている点に注意。)
表より、3けたのヘビ数は328個あります。
4けたの場合もまったく同じ考え方で個数を数えることができます。
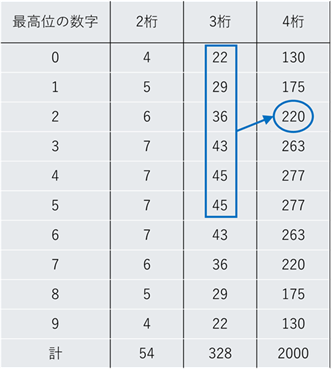
(青枠は「2???の個数」の計算例。)
表より、2000未満のヘビ数の個数は54+328+175=557個。
2000~2025のヘビ数の個数は、4+5+6=15個(0?と1?と2?の個数の合計)。
よって、2025は557+15=572番目のヘビ数です。
また、7000未満のヘビ数の個数は、6???までを合計して、
54+328+175+220+263+277+277+263=1857個
74??が45個あるので、その中で最大の7479が1857+45=1902番目。
75??が45個あるので、その中で最大の7589が1902+45=1947番目。
76??が43個あるので、その中で最大の7699が1947+43=1990番目。
77??が36個あるので、その中で最大の7799が1990+36=2026番目。
よって、2025番目は7799の1つ前のヘビ数、すなわち7798です。